Expected Value When You Must Roll Again

Well, the question is more complex than information technology seems at first glance, but you'll shortly encounter that the answer isn't that scary! It's all well-nigh maths and statistics.

First of all, we have to determine what kind of dice roll probability we want to detect. Nosotros tin can distinguish a few which yous can detect in this dice probability calculator.

Before we make any calculations, let's define some variables which are used in the formulas. n - the number of dice, due south - the number of an individual dice faces, p - the probability of rolling any value from a dice, and P - the overall probability for the problem. There is a elementary human relationship - p = 1/south, so the probability of getting 7 on a 10 sided die is twice that of on a 20 sided dice.

1. The probability of rolling the same value on each die - while the take a chance of getting a particular value on a unmarried die is p, we only need to multiply this probability past itself as many times as the number of dice. In other words, the probability P equals p to the power northward, or P = pⁿ = (i/south)ⁿ. If we consider three 20 sided dice, the chance of rolling 15 on each of them is: P = (1/20)³ = 0.000125 (or P = one.25·10⁻⁴ in scientific notation). And if y'all are interested in rolling the set of any identical values, simply multiply the result by the full die faces: P = 0.000125 * 20 = 0.0025.

2. The probability of rolling all the values equal to or higher than y - the problem is similar to the previous one, simply this time p is 1/s multiplied past all the possibilities which satisfy the initial condition. For case, allow's say we accept a regular die and y = 3. We desire to rolled value to be either 6, 5, 4, or 3. The variable p is then four * ane/vi = 2/three, and the final probability is P = (ii/iii)ⁿ.

3. The probability of rolling all the values equal to or lower than y - this pick is about the aforementioned as the previous one, but this time we are interested but in numbers which are equal to or lower than our target. If we take identical weather condition (s=six, y=3) and apply them in this example, we can see that the values 1, 2, & 3 satisfy the rules, and the probability is: P = (3 * ane/six)ⁿ = (one/2)ⁿ.

4. The probability of rolling exactly X aforementioned values (equal to y) out of the ready - imagine you have a gear up of seven 12 sided dice, and yous want to know the chance of getting exactly ii 9s. It's somehow different than previously because only a part of the whole set has to match the weather. This is where the binomial probability comes in handy. The binomial probability formula is:

P(X=r) = nCr * pʳ * (1-p)ⁿ⁻ʳ,

where r is the number of successes, and nCr is the number of combinations (also known equally "north choose r").

In our example we accept n = 7, p = 1/12, r = ii, nCr = 21, then the last result is: P(X=2) = 21 * (i/12)² * (11/12)⁵ = 0.09439, or P(X=2) = 9.439% equally a percentage.

5. The probability of rolling at to the lowest degree X same values (equal to y) out of the set - the problem is very similar to the prior one, but this time the outcome is the sum of the probabilities for X=2,3,4,5,vi,7. Moving to the numbers, nosotros have: P = P(10=ii) + P(X=3) + P(X=4) + P(Ten=5) + P(X=6) + P(X=7) = 0.11006 = 11.006%. As you lot may expect, the outcome is a little higher. Sometimes the precise wording of the problem will increment your chances of success.

6. The probability of rolling an verbal sum r out of the set of n south-sided die - the general formula is pretty circuitous:

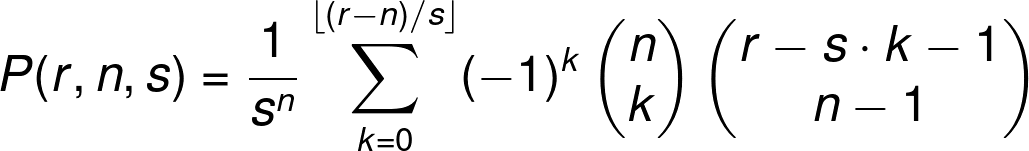
Even so, we tin can also try to evaluate this problem by paw. One approach is to find the total number of possible sums. With a pair of regular dice, we can have ii,3,four,5,half dozen,7,viii,nine,x,11,12, but these results are non equivalent!

Take a look, in that location is only one way you can obtain 2: 1+one, but for 4 there are 3 different possibilities: one+iii, 2+2, three+1, and for 12 at that place is, once again, only one variant: 6+6. It turns out that 7 is the nearly likely result with half-dozen possibilities: 1+half-dozen, 2+5, 3+4, 4+iii, five+two, 6+1. The number of permutations with repetitions in this set is 36. We can estimate the probabilities every bit the ratio of favorable outcomes to all possible outcomes: P(two) = one/36, P(4) = three/36 = 1/12, P(12) = 1/36, P(seven) = 6/36 = ane/6.

🔎 Our ratio calculator can be quite helpful in finding the missing term of such ratios!

The higher the number of dice, the closer the distribution function of sums gets to the normal distribution. Every bit you may expect, every bit the number of dice and faces increases, the more time is consumed evaluating the effect on a sheet of paper. Luckily, this isn't the case for our die probability calculator!

7. The probability of rolling a sum out of the set, not lower than X - like the previous trouble, we accept to detect all results which match the initial condition, and divide them by the number of all possibilities. Taking into account a set of three x sided die, we want to obtain a sum at least equal to 27. As we can come across, we take to add together all permutations for 27, 28, 29, and 30, which are 10, 6, three, and 1 respectively. In total, there are 20 good outcomes in 1,000 possibilities, so the final probability is: P(X ≥ 27) = 20 / i,000 = 0.02.

8. The probability of rolling a sum out of the set, not higher than X - the procedure is precisely the aforementioned every bit for the prior job, but we have to add together only sums below or equal to the target. Having the same set of dice as above, what is the chance of rolling at nigh 26? If you were to practice it step by step, it would accept ages to obtain the result (to sum all 26 sums). But, if you think about it, we have merely worked out the complementary event in the previous problem. The full probability of complementary events is exactly 1 , so the probability here is: P(10 ≤ 26) = 1 - 0.02 = 0.98.

dobsonalienighted.blogspot.com

Source: https://www.omnicalculator.com/statistics/dice

Share this post